本文目录
一元二次方程解有三种情况:无解,两个解相等,有两个不同解。这三种情况与啥有关?
一元二次方程解有三种情况:无解^2-4ac
两个解相等:b^2-4ac=0;
有两个不同解:b^2-4ac>0。
这三种情况都与(得尔他)即b^2-4ac有关。
一元二次方程基本解法结果形式?
1、一元二次方程公式一般形式:ax2+bx+c=0(a≠0)。
2、其中ax2叫作二次项,a是二次项系数;bx叫作一次项,b是一次项系数;c叫作常数项。
3、只含有一个未知数(一元),并且未知数项的最高次数是2(二次)的整式方程叫做一元二次方程!
一元二次方程的四种公式?
1、直接开平方法;2、 *** 法;3、公式法;4、因式分解法。
一元二次方程的一般形式为:ax^2(2为次数,即X的平方)+bx+c=0, (a≠0),它是只含一个未知数,并且未知数的最高次数是2 的整式方程。
解一元二次方程的基本思想方法是通过“降次”将它化为两个一元一次方程。一元二次方程有四种解法:
1、直接开平方法;2、 *** 法;3、公式法;4、因式分解法。
一元二次无解的判别式?
一元二次方程ax2+bx+c=0的判别式=b2-4ac
这个判别式是根据方程的求根公式得来的,因为
ax2+bx+c=0===>a(x+b/2a)2-b2/4a+c=0===>x=[-b±√(b2-4ac)]/2a
从求根公式可以看出,b2-4ac的结果决定了方程是否具有实数根,或具有什么样的实数根,所以,就称b2-4ac为一元二次方程的判别式,符号△
(1)当△=0时,方程具有一个实数根(或两个相等实数根)
(2)当△<0时,方程无解
(3)当△>0时,方程具有两个不相等实数根
根据求根公式和判别式,推导出韦达定理
假设一元二次方程具有两个实数根x1、x2,则这两个实数根的关系为:
x1+x2=[-b+√△]/2a+[-b-√△]/2a=-b/a
x1x2=[-b+√△]/2a×[-b-√△]/2a=c/a
当然,上述条件成立(包括判别式)的首要条件是a≠0
10道一元二次方程及答案?
1)求x^2一3x一18二0的解,(x二6,x二一3),
2)解方程3x^2十x十1二0,(▽<0,无解),
3)已知方程二根为2,3,求方程x^2十bx十c中b,c。(一5,6),
4)已知方程x^2十bx十8=o的一个根为2,求另一根和b,(4,一6),
5)方程x^2二4,求根,(2,一2),
6)方程x^2十6x二o,求根(0,一6),
7)己知y二ax^2十bx十C与x轴两交点的横坐标互为倒数,且中点为2,求方程ax^2十bx十c二0的解,(2十√3,2一√3),
8)己知方程一根是另一根的相反数,方程ax^2十bx十C二0中b。(0)
9)不等式ax^2十bx十C<0的解是一3≤x≤5,求方程ax^2十bx十C二0的解,(一3,5),
10)解方程3x^2十2x一1二0,(1/3,一1)。老师,我看有好多题有误,如有需要,我可以提供部分题,如同意给我发题方法或如何发给你。



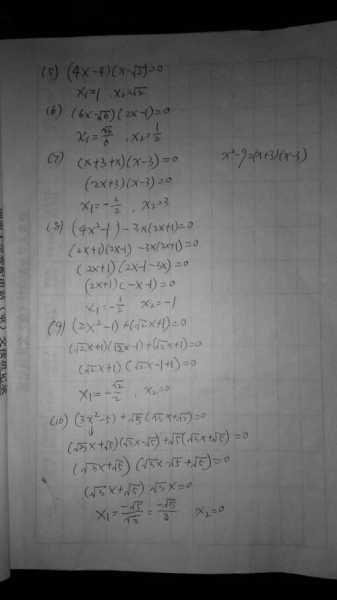




还没有评论,来说两句吧...